CSS Transformsについてのメモ
公開:
更新:
既に色々なデモページが作られていたり、実用されていたりするCSS Transformsですが、ちゃんと理解したかったので調べてみました。
まだそんなに自信はありませんが、以前よりは理解できた気がします。
というわけなので、自分が分かる範囲で説明してみたいと思います。
CSS Transformsは2Dと3Dとで別になっていますが、将来的には SVG Transforms と合わせて一つの仕様になるそうです。
今はまだ別々なので、それぞれにリンクをしておきます。括弧内は現時点での最新の日付です。
- WD: CSS 2D Transforms(2011/12/15)
- ED: CSS Transforms(2011/11/28)
- WD: CSS 3D Transforms Module Level 3(2009/03/20)
- ED: CSS 3D Transforms(2011/03/21)
新しくなった仕様が出ていましたので、リンクを追加しておきます。最新版へのリンクです。
記事内容に若干の不安があるので、他力本願で申し訳ないですが間違っていたら教えていただけると助かります。 どのような変形を行うかを指定します。指定はTransform関数で行います。 初期値は 以下はサンプルです。 要素の拡大縮小を行います。 要素を回転させます。回転の方向は時計回りです。 要素を傾斜させます。 transform: skewX() & transform: skewY() sample 行列を使用して変形を指定します。これ1つで上記の指定をまとめて行うこともできます。 この関数には6つのパラメータがあり、変形なしの状態だと 使用される行列は3×3ですが、うち3つは固定です。 変形なしの状態の行列はこうなります。 この行列が何をするのかですが、この行列を使って座標を算出します。 これを計算します。 この たとえば、100×100の要素を 次に、ここまで出てきた関数を行列に変換してみます。 また、 仮に、 実際に試して見ましょう。 これを重ねてみます。 transform: matrix() sample 2 値が1つしかない場合、2つ目の値は 値が2つの場合、その値がキーワードでなければ、1つ目の値は水平方向、2つ目の値は垂直方向のものとして扱われます。 値が3つ、または4つの場合、<percentage>や<length>の前にキーワードが先行する必要があります。 正の値は、ボーダーボックスの端から内側へのオフセットを、負の値はボーダーボックスの端から外側へのオフセットを表します。 このプロパティの初期値は 次のサンプルは、赤い部分を 2D Transformsについては以上です。 Transformsを使うことで、要素を2次元または3次元へ移動・回転・スケール変更することができます。 3次元空間ではZ軸が追加され、その正の値はウィンドウからユーザー側に向かって伸びており、負の値はユーザー側からウィンドウに向かってより奥に伸びています。 ちょっと斜め上から見たらこんな感じです。文字が書かれているほうが負になります。 それと、ここから先で使うサンプルですが、変形の確認に使う基本のHTMLとCSSはこんな感じになっています。 また、正面からだと変形したことが分かりにくいものもありますので、斜め上から見ているような感じにしていますが、画面上のほうにあるボタンで切り替えられます。 2D Transformsと同様、どのような変形を行うかを指定します。指定はTransform関数で行います。 初期値は 3Dでの要素の移動を行います。 以下はサンプルです。 transform: translate3d() sample 移動を個別に指定します。 パラメータには<length>または<percentage>ですが、 3Dでの要素の拡大縮小を行います。指定には<number>形式を使用します。 X方向、Y方向への比率が変化しているのが分かります。ですが、Z軸については何も変化していないように見えます。Z方向へ拡大するからといって、要素に厚みが出るわけではありません。 と、なっています。 回転されたものが、Z方向にも変化しているのが分かります。 要素を3D回転させます。 またこの関数は、 各ベクトルごとに回転を指定します。パラメータは<angle>形式で記述します。 同様に 回転の中心となるポイントは transform: rotateX() rotateY() rotateZ() sample 要素を傾斜させます。 要素の傾斜をX方向、Y方向と個別に指定する関数です。 透視投影による指定をします。これを指定することにより、変形に遠近効果をつけることができます。遠くのものはより小さく、近くのものはより大きく、といった感じです。 仕組みとしては、視点のポイントから要素の4つの各頂点を線で結び、その線の 綺麗な図が描けなかったので真横からの図になりますが、次のような感じです。 関数の指定については<length>形式で記述するとなっていますが、px以外で指定しているものを見たことがないです……。 指定する値は また、 transform: perspective() sample 行列による指定を行います。この行列は座標変換を行うためのものです。 この関数は16個のパラメータがあり、変形なしの状態だと 変形なしだとこうなります。 ちなみに、 これらを計算するときには、角度 変形の原点を指定します。原点の座標は、要素の左上 指定は2D Transformsのときと同様ですが、Z方向場合にはパーセンテージとキーワードは使用できません。 次のサンプルは、赤い部分を このプロパティは、指定した子要素が3D空間上で平面として描画されるか、立体として表示されるかを指定します。 指定できる値は 次のサンプルは、各サンプルの親要素に transform-style sample 同様に、指定には<length>形式を用い、 初期値は 2つ目の値が省略され、1つ目の指定がキーワードでなければ、もう1つの値は 仮に、Z軸の負の方向に移動した要素の親要素に 以下のサンプルは、赤い色のボックスが perspective-origin sample 正面から見ると次のようになります。 値には backface-visibility sample このプロパティに指定する各関数ですが、指定するときは順番に注意したほうがいいかと思います。 基本的に行列の乗算には交換法則が成り立ちませんので、行列 とりあえずは、 上の関数の書き順にも関係してくるのですが、変形のない状態の場合、見た目の上ではX軸は左から右へ、Y軸は上から下へ、Z軸は奥から手前へ、と数値が増えていきます。 練習を兼ねてアニメーションしながら回転する立方体を作ってみます。 実際にはプロパティごとに各ベンダープレフィクスが必要となりますが、記事内には書きません。 3D変形させるのは CSS Cube 1 次に、各パネルを回転させ、立方体になったとき、表が外側に来るようにします。 CSS Cube 2 正面からだとあまり変化がないように見えますが、ちょっと斜め上から見ると次のようになります。 それでは、立方体にするために各パネルを移動します。 CSS Cube 3 立方体ができました。 CSS Cube 4 アニメーションができました。 CSS Cube 5 何か変ですね。ではなぜこうなったのか考えてみます。 パネルが立方体を作るための変形(回転と移動)をする際、親要素で指定されたPerspectiveが加わります。それは全ての子要素から見て同じ位置であり、親要素の ではどうすればいいのかというと、 CSS Cube 6 期待通りの動きになりました。 これで無事に回転する立方体が完成しました。 いつものことですが、この記事を鵜呑みにせず、自分でも仕様を確認したり、実際に試してブラウザの調査ツールなどで調べてみたりしてください。 最後まで読んでいただき、ありがとうございました。CSS 2D Transforms
transformプロパティ
関数は空白区切りにより複数指定できます。
各関数は指定した順に適用されます。noneです。translate(tx, ty)translate()では、要素の移動を行います。
1つ目のパラメータでX方向への移動距離、2つ目のパラメータでY方向への移動距離を指定します。
2つ目のパラメータtyが省略された場合、tyは0として計算されます。
指定には<length>形式、または<percentage>を使用します。
灰色の部分が変形適用前のもの、赤い部分が適用後のものとなります。.sample1 {
transform: translate(0);
}
.sample2 {
transform: translate(20px);
}
.sample3 {
transform: translate(20px, 20px);
}
translateX(), translateY()translate()を個別に指定する関数です。translateX()はX方向へ、translateY()はY方向への移動距離を指定します。scale(sx, sy)
1つ目のパラメータでX方向の比率を、2つ目のパラメータでY方向の比率を指定します。
2つ目のパラメータsyが省略された場合、syは1つ目のパラメータsxと同じ値として計算されます。
また、指定には<number>形式を使用します。.sample1 {
transform: scale(0);
}
.sample2 {
transform: scale(1.2);
}
.sample3 {
transform: scale(1.2, 0.8);
}
scaleX(), scaleY()scale()を個別に指定する関数です。scaleX()でX方向、scaleY()でY方向の比率を指定します。
仮にscaleX()しか指定されていない場合、残るscaleY()の値は1となります。これは逆の場合でも同じです。rotate()
回転の中心点はtransform-origin(後述)プロパティで指定されたポイントとなります。
パラメータは1つだけで、<angle>形式で指定します。.sample1 {
transform: rotate(0);
}
.sample2 {
transform: rotate(15deg);
}
.sample3 {
transform: rotate(-15deg);
}
skewX(), skewY()skewX()はX軸に沿って指定された分の傾斜を与えます。同様に、skewY()はY軸に沿います。
パラメータは1つだけで、<angle>形式で指定します。.sample1 {
transform: skewX(0);
}
.sample2 {
transform: skewX(15deg);
}
.sample3 {
transform: skewY(15deg);
}
matrix(a, b, c, d, e, f)
非常にややこしいのでCSSしか書かない人が使う機会は少ないかもしれませんが、JavaScriptで変形を操作するときには必要になってきたりします。CSS でrotate()やscale()などを使って書いたとしても、JavaScriptからtransformの値を取得すると、このmatrix()になるからです。matrix(1, 0, 0, 1, 0, 0)となります。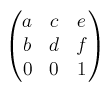
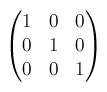
要素の4つの頂点(要素は矩形なので)を、それぞれ(X, Y, 1)とし、これを行列に乗算して座標を出します。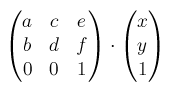
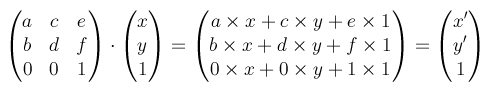
x’とy’が変形後の座標になります。
これを各頂点ごとに行い、それぞれの結果に応じて要素の頂点の座標を移動することで変形が行われます。translate(10, 20)すると、次のようになります。
上から順に、左上、右上、左下、右下の頂点です。
translate()からmatrix()へtranslate(tx, ty)はmatrix(1, 0, 0, 1, tx, ty)で表せます。translateX(tx), translateY(ty)でも同様です。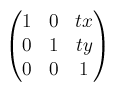
scale()からmatrix()へscale(sx, sy)はmatrix(sx, 0, 0, sy, 0, 0)で表せます。scaleX(sx), scaleY(sy)でも同様です。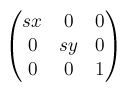
rotate()からmatrix()へrotate(a)はmatrix(cos(a), sin(a), -sin(a), cos(a), 0, 0)で表せます。aは角度で、度数法(degree)ではなく弧度法(radian)で指定します。
たとえば90degの場合、90 * π / 180 = 1.570796325 [rad]となります。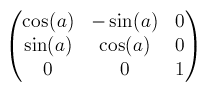
skewX(), skewY()からmatrix()へskewX(a)はmatrix(1, 0, tan(a), 1, 0, 0)で表せます。aはrotate()のときと同じです。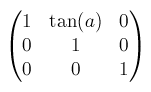
skewY(a)はmatrix(1, tan(a), 0, 1, 0, 0)で表せます。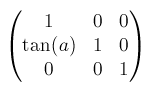
複数指定されている場合
rotate(30deg) scale(2) translate(10px, 10px)といった指定があったとしましょう。
この場合には、次のようになります。
(四捨五入しています)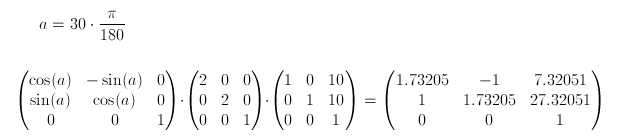
matrix()でまとめて指定するとmatrix(1.73205, 1, -1, 1.73205, 7.32051, 27.32051)となります。
計算方法はめんどくさいので行列の乗算の方法を調べてください。
計算するだけなら「Web 2.0 scientific calculator」などを使うと楽です。.sample1 {
transform: rotate(30deg) scale(2) translate(10px, 10px);
}
.sample2 {
transform: matrix(1.73205, 1, -1, 1.73205, 7.32051, 27.32051);
}

transform-originプロパティtransform-originでは、変形の原点を指定できます。
指定には、<percentage>と<length>、キーワードが使えます。
キーワードは、水平方向の場合left, center, rightで、垂直方向の場合はtop, center, bottomとなります。centerとして扱われます。
<percentage>と<length>は、要素のボーダーボックスの左上隅からのオフセットを表します。
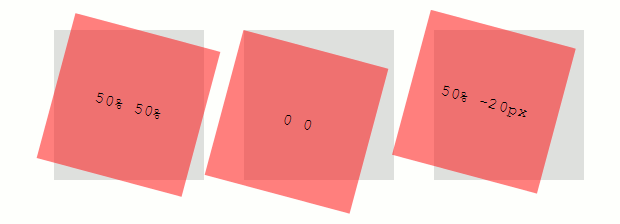
たとえば、transform-origin: bottom 10px right 20pxは、垂直方向が要素の下端から10px、水平方向が右端から20pxの位置になります。値が3つしかない場合、未指定のオフセットは0であるとみなされます。50% 50%です。transform: rotate(15deg)し、transform-originの値を変更したものです。.sample1 {
transform-origin: 50% 50%;
}
.sample2 {
transform-origin: 0 0;
}
.sample3 {
transform-origin: 50% -20px;
}
CSSアニメーションとの絡み、DOMでの扱いなどは仕様に載っていますので参照してください。CSS 3D Transforms
Perspective transformは、奥行きのある表現を可能にします。
Z軸を真横から見た場合、ユーザー側が正の値、その逆が負の値となります。
(文字も回転しちゃってますが気にしないでください)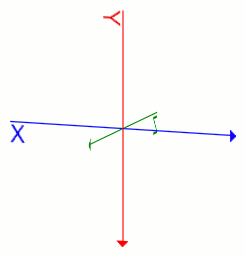
<div class="drawing">
<h2>...</h2>
<div class="box">
<div class="base"></div>
<div class="sample"></div>
</div>
</div>.box {
position : relative;
width : 200px;
transform: rotateX(-10deg) rotateY(-20deg);
}
.base,
.base + div {
position: absolute;
top : 50px;
left : 50px;
width : 100px;
height : 100px;
}
軸も表示していますが、これも表示・非表示を切り替えられます。transformプロパティ
関数は空白区切りにより複数指定できます。
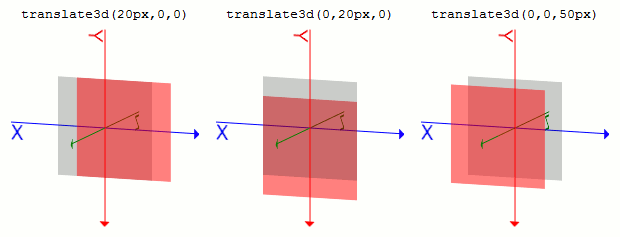
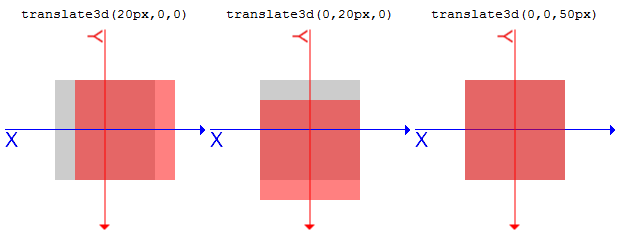
また、各関数は指定した順に適用されます。noneです。translate3d(tx, ty, tz)
指定には<length>形式、または<percentage>を使用しますが、Z方向では<length>のみが使用できます。
灰色の部分が変形適用前のもの、赤い部分が適用後のものとなります。.sample1 {
transform: translate3d(20px, 0, 0);
}
.sample2 {
transform: translate3d(0, 20px, 0);
}
.sample3 {
transform: translate3d(0, 0, 50px);
}
translateX(tx), translateY(ty), translateZ(tz)translateX(tx)はtranslate3d(tx, 0, 0)と同じです。
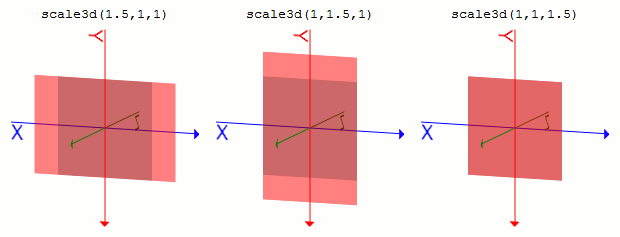
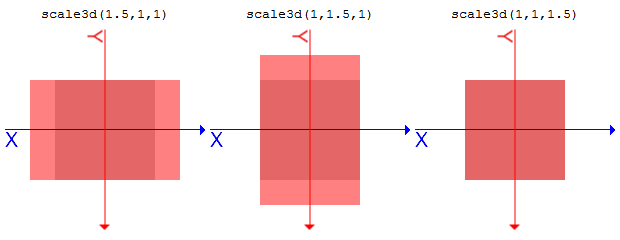
同様に、translateY(ty)はtranslate3d(0, ty, 0)と同じ、translateZ(tz)はtranslate3d(0, 0, tz)と同じになります。translateZ()の場合<percentage>は使えません。scale3d(sx, sy, sz).sample1 {
transform: scale3d(1.5, 1, 1);
}
.sample2 {
transform: scale3d(1, 1.5, 1);
}
.sample3 {
transform: scale3d(1, 1, 1.5);
}
では、Z方向へ拡大したものをY軸を中心に少し回転させてみましょう。
(回転については次の次のセクションからやります).sample1 {
transform: scale3d(1, 1, 1) rotateY(45deg);
}
.sample2 {
transform: scale3d(1, 1, 1.5) rotateY(45deg));
}
.sample3 {
transform: scale3d(1.5, 1, 1.5) rotateY(45deg);
}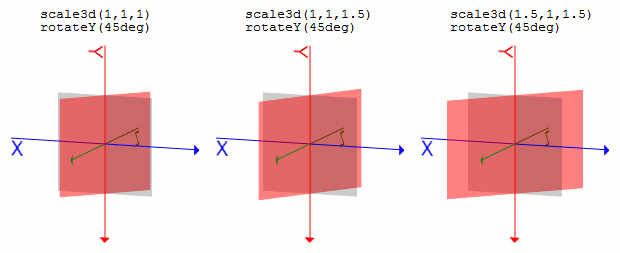
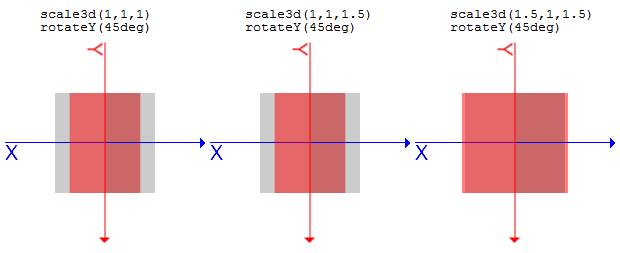
scale3d(1, 1, sz)はZ方向に変化のある要素のZ方向の比率が変更される、ということです。scaleX(sx), scaleY(sy), scaleZ(sz)scale3d()の各パラメータを個別に指定する関数です。scaleX(sx)はscale3d(sx, 1, 1)と、scaleY(sy)はscale3d(1, sy, 1)と、scaleZ(sz)はscale3d(1, 1, sz)と同じになります。rotate3d(x, y, z, a)x, y, zで方向ベクトルを指定し、aで回転の角度を指定します。回転は時計回りに行われます。
回転はtransform-originで指定したポイントを基準に行われまれ、角度の指定は <angle>形式で記述します。matrix3d(1+(1-cos(angle))*(x*x-1), -z*sin(angle)+(1-cos(angle))*x*y, y*sin(angle)+(1-cos(angle))*x*z, 0, z*sin(angle)+(1-cos(angle))*x*y, 1+(1-cos(angle))*(y*y-1), -x*sin(angle)+(1-cos(angle))*y*z, 0, -y*sin(angle)+(1-cos(angle))*x*z, x*sin(angle)+(1-cos(angle))*y*z, 1+(1-cos(angle))*(z*z-1), 0, 0, 0, 0, 1)と等しくなります。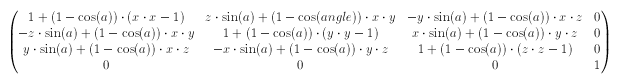
.sample1 {
transform: rotate3d(1, 0, 0, 45deg);
}
.sample2 {
transform: rotate3d(0, 1, 0, 45deg);
}
.sample3 {
transform: rotate3d(0, 0, 1, 45deg);
}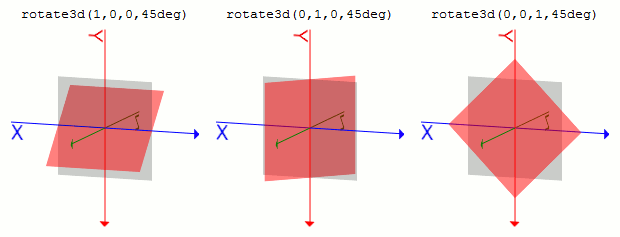
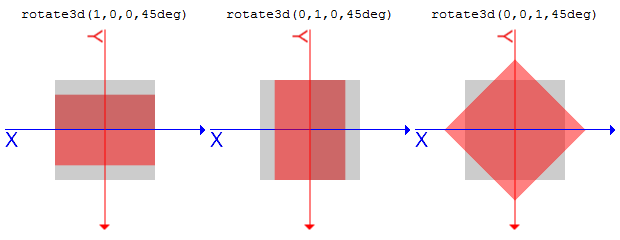
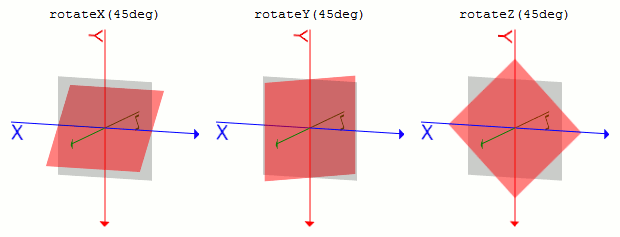
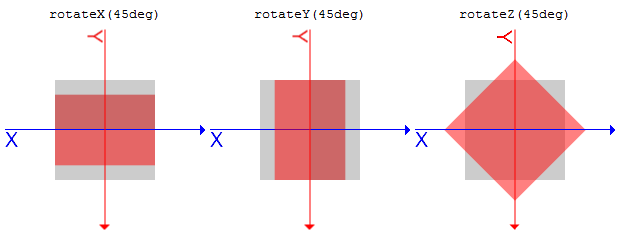
rotateX(a), rotateY(a), rotateZ(a)rotate3d()でまとめて指定しようとするとややこしいので、CSSを書く人はこちらをメインに使うことになるかと思います。rotateX(a)では、aに指定された角度だけ、X軸を基準に要素を時計回りに回転させます。rotateX(a)はrotate3d(1, 0, 0, a)と同じ変形となります。rotateY(a)はrotate3d(0, 1, 0, a)とrotateZ(a)はrotate3d(0, 0, 1, a)と同じ変形となります。
回転の基準となる軸もそれぞれY軸・Z軸となります。transform-originで指定した座標になります。.sample1 {
transform: rotateX(45deg);
}
.sample2 {
transform: rotateY(45deg);
}
.sample3 {
transform: rotateZ(45deg);
}
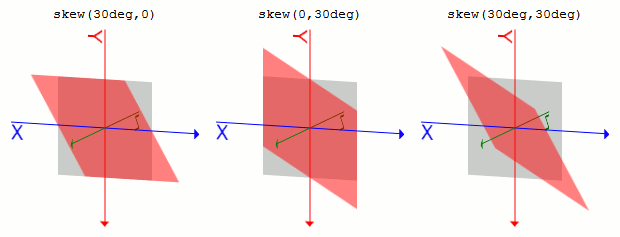
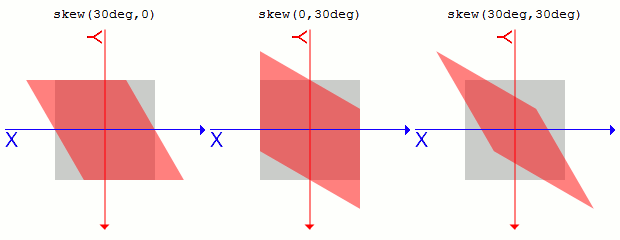
skew(ax, ay)
1つ目のパラメータでX方向の、2つ目のパラメータでY方向の傾斜を指定します。
2つ目のパラメータが指定されていない場合、0として扱われ、Y方向の変形は行われません。 パラメータは<angle>形式で記述します。.sample1 {
transform: skew(30deg, 0);
}
.sample2 {
transform: skew(0, 30deg);
}
.sample3 {
transform: skew(30deg, 30deg);
}
skewX(a), skewY(a)
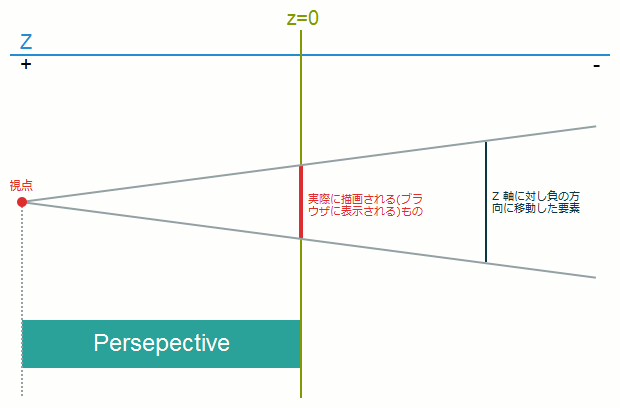
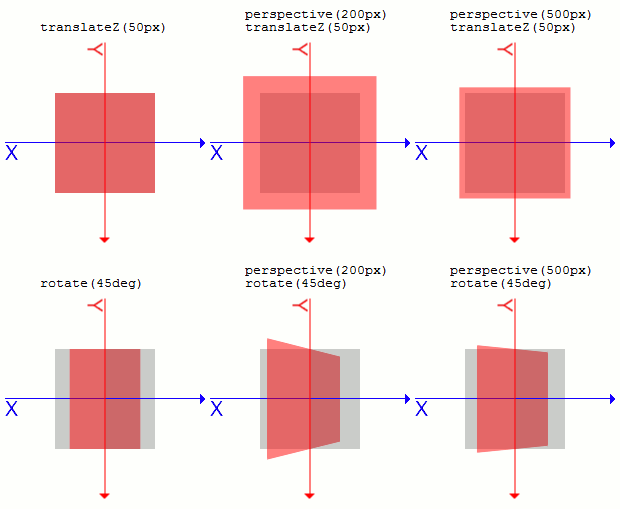
パラメータは<angle>形式で記述します。skewX(a)はskew(a, 0)とskewY(a)はskew(0, a)と同じ変形となります。perspective(d)z=0の位置に描画されるものがブラウザで閲覧する変形後の要素となります。
たとえばZの位置が小さいほど、線同士が作る角度は狭くなるので、より小さく描画されます。
このperspective()はz=0から視点ポイントまでの距離を指定します。
CSS TransformsでいうところのtranslateZ()だけを指定した要素で、結ばれている線は実際には頂点ごとに、つまり4本あると思ってください。
「Z方向に対し正(負)の方向に移動した要素」自体の大きさは同じです。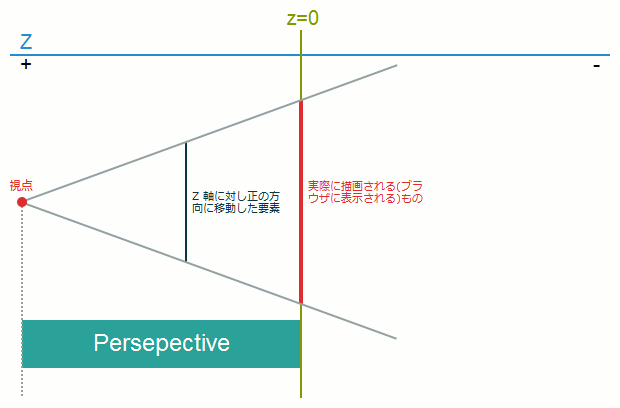
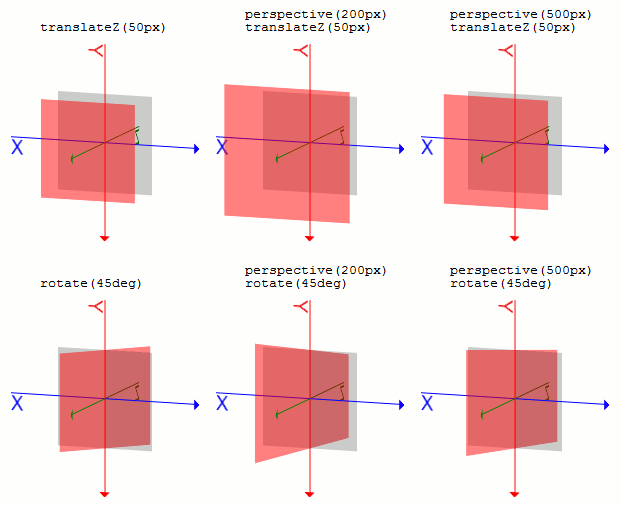
数値の大小による見え方の違いですが、数値が小さいほど遠近感が強く、大きいほど遠近感が弱くなります。0より大きい値である必要があります。perspective()が指定されていない場合、要素の各頂点からz=0への線がz=0に対して垂直になるように投影されます。.sample1 {
transform: translateZ(50px);
}
.sample2 {
transform: perspective(200px) translateZ(50px);
}
.sample3 {
transform: perspective(500px) translateZ(50px);
}
.sample4 {
transform: rotateY(45deg)
}
.sample5 {
transform: perspective(200px) rotateY(45deg)
}
.sample6 {
transform: perspective(500px) rotateY(45deg)
}
matrix3d(a1, b1, c1, d1, a2, b2, c2, d2, a3, b3, c3, d3, a4, b4, c4, d4)
座標変換のやり方はは2Dのときと同じです。matrix3d(1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1)となります。matrix3d()では 4×4の次のような行列を使います。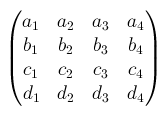
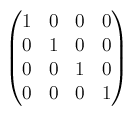
matrix(a, b, c, d, e, f)をmatrix3d()で表すと、matrix3d(a, b, 0, 0, c, d, 0, 0, 0, 0, 1, 0, e, f, 0, 1)となります。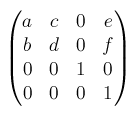
translate3d()からmatrix3d()へtranslate3d(tx, ty, tz)はmatrix3d(1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, tx, ty, tz, 1)で表せます。translateX(tx)はtranslate3d(tx, 0, 0)なので、同じように当てはめるといいです。これはtranslateY(ty), translateZ(tz)でも同様です。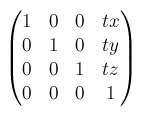
scale3d()からmatrix3d()へscale3d(sx, sy, sz)はmatrix3d(sx, 0, 0, 0, 0, sy, 0, 0, 0, 0, sz, 0, 0, 0, 0, 1)で表せます。scaleX(sx)はscale3d(sx, 1, 1)なので、同じように当てはめるといいです。これはscaleY(sy), scaleZ(sz)でも同様です。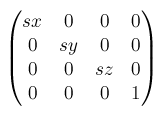
rotate3d()からmatrix3d()へrotate3d(x, y, z, a)は、その関数の項目で書いたようにmatrix3d(1+(1-cos(angle))*(x*x-1), -z*sin(angle)+(1-cos(angle))*x*y, y*sin(angle)+(1-cos(angle))*x*z, 0, z*sin(angle)+(1-cos(angle))*x*y, 1+(1-cos(angle))*(y*y-1), -x*sin(angle)+(1-cos(angle))*y*z, 0, -y*sin(angle)+(1-cos(angle))*x*z, x*sin(angle)+(1-cos(angle))*y*z, 1+(1-cos(angle))*(z*z-1), 0, 0, 0, 0, 1)となります。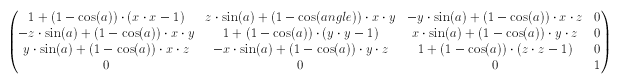
rotateX(), rotateY(), rotateZ()からmatrix3d()へaをradianで計算します。
2Dのmatrix()でも触れましたが、degreeaはa * π / 180でradianに変換できます。rotateX()はmatrix3d(1, 0, 0, 0, 0, cos(a), sin(a), 0, 0, -sin(a), cos(a), 0, 0, 0, 0, 1)となります。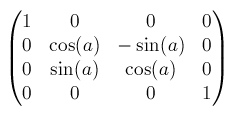
rotateY()はmatrix3d(cos(a), 0, sin(a), 0, 0, 1, 0, 0, -sin(a), 0, cos(a), 0, 0, 0, 0, 1)となります。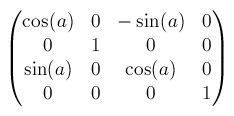
rotateZ()はmatrix3d(cos(a), sin(), 0, 0, -sin(a), cos(a), 0, 0, 0, 0, 1, 0, 0, 0, 0, 1)となります。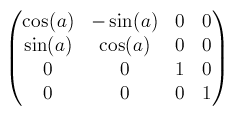
skew()からmatrix3d()へskew(ax, ay)は、matrix3d(1, tan(ay), 0, 0, tan(ax), 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1)となります。skewX(ax), skewY(ay)で個別に指定するときも同様です。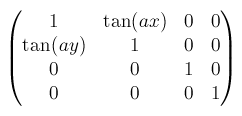
perspective()からmatrix3d()へperspective(d)は、matrix3d(1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, -1/d, 0, 0, 0, 1)となります。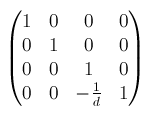
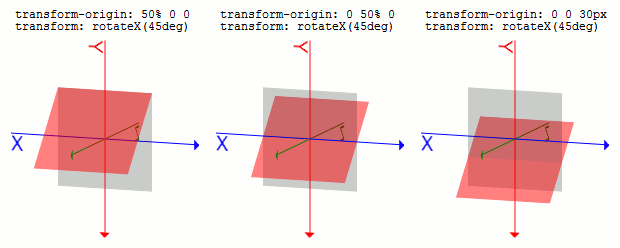
transform-originプロパティ(0, 0, 0)からの距離となります。
初期値は50% 50% 0です。transform: rotateY(45deg)し、transform-originの値を変更したものです。.sample1 {
transform-origin: 50% 0 0;
}
.sample2 {
transform-origin: 0 50% 0;
}
.sample3 {
transform-origin: 0 0 50px;
}
transform-styleプロパティflatまたはpreserve-3dで、初期値はflatです。flatを指定すると、3D空間上で平面として描画され、preserve-3dを指定すると、立体的に表示されます。transform-styleプロパティでflat, preserve-3dを指定したものです。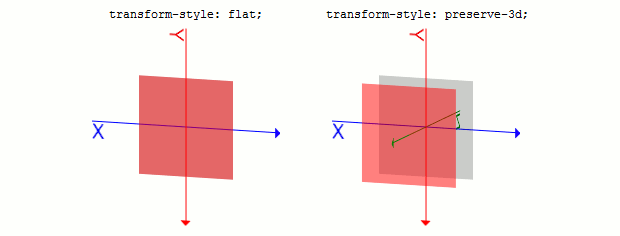
flatを指定した1つ目の例ではZ方向のものも平面になっているのが分かります。perspectiveプロパティtransformプロパティで使うperspective()関数と同じ意味です。
違いは、perspective()関数が要素そのものの深度を指定するのに対し、このperspectiveプロパティでは、指定した要素の子要素全体の深度を指定することにあります。0より大きい値を指定しなければなりません。perspective-originプロパティperspectiveプロパティの視点ポイントの位置を指定します。値は2つあり、X方向Y方向の座標を指定します。
値にはtransform-originと同様に、<percentage>と<length>、キーワードが使えます。
キーワードは、水平方向の場合left, center, rightで、垂直方向の場合はtop, center, bottomとなります。0 0は要素の左上の座標です。50% 50%です。50%として扱われます。
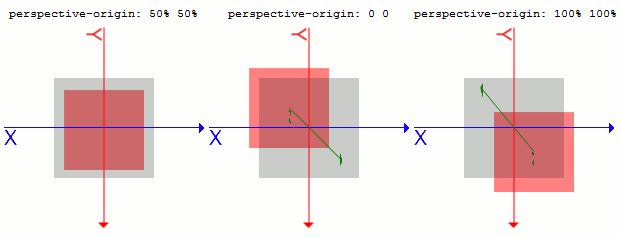
1つ目がX方向のキーワードの場合は、Y方向は50%となり、Y方向のキーワードの場合はX方向が50%として扱われます。perspectiveを指定し、perspective-originのY方向の値を増やすと、次のような図になります。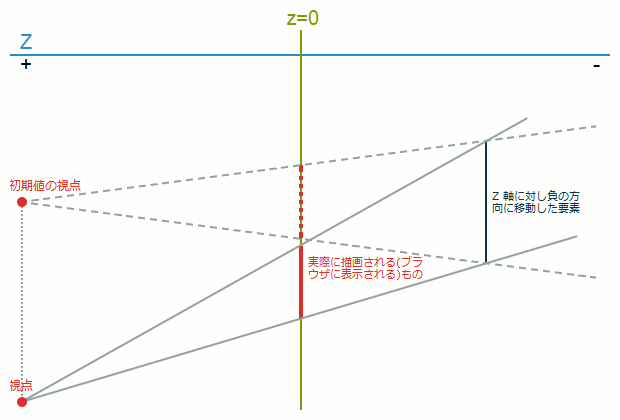
transform: translateZ(-100px)されたもので、全ての親要素に、perspective: 500が指定されており、さらに、親要素にperspective-originがそれぞれ50% 50%, 0 0, 100% 100%と指定されたものです。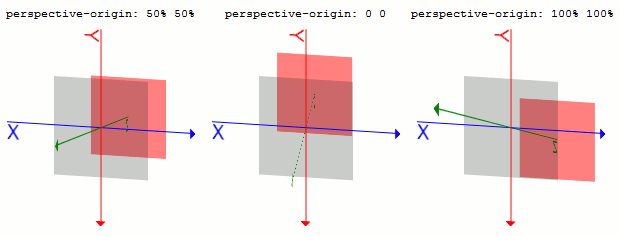
backface-visibilityプロパティbackface-visibilityプロパティは、要素の裏側を表示するかどうかを指定するプロパティです。hiddenとvisibleが使用可能で、初期値はvisibleとなっています。hiddenを指定すると、要素の表面が見えなくなった(たとえばrotateY(180deg)された)場合に、その要素は見えなくなります。visibleの場合は、その要素を裏側から透かして見るような感じになります。transform: rotateY(180deg)した要素のbackface-visibilityプロパティに、それぞれhidden, visibleを指定すると次のようになります。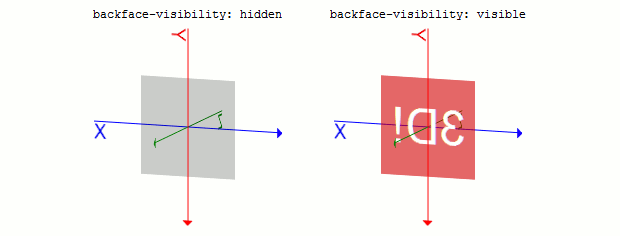
transformプロパティでの注意点
変形の最終的な座標は行列によって計算されるわけですが、仮にtransform: 関数A 関数Bという変形を行うとすると、関数Aの行列 * 関数Bの行列となり、そこから座標が計算されるということです。AとBがあるとき、A*BとB*Aは別物となります。transformプロパティに指定する関数は書いた順に適用される、と覚えておけばいいと思います。3Dでの回転について
ですが3D Transformsにおいて回転変形を行うと、その要素の各軸は回転に伴って移動します。たとえば、rotateY(180deg)すると、その要素は裏返したような状態になりますが、このときX軸は右から左へ、Z軸は手前から奥へ、となります。transform: rotate(180deg)したものを奥にあるように見せるには、rotate(180deg) translateZ(100px)とします。translateZ(100px) rotate(180deg)では手前側に移動した後に回転となるので、手前側にあるように見えます。translateZ()を先に書くなら、translateZ(-100px) rotate(180deg)とします。回転する立方体を作ってみる
まず、ベースとなる部分から。
あまり関係ない部分も省略しています。<div class="drawing">
<div class="cube">
<div class="panel front">1</div>
<div class="panel back">2</div>
<div class="panel left">3</div>
<div class="panel right">4</div>
<div class="panel top">5</div>
<div class="panel bottom">6</div>
</div>
</div>
.drawing {
width : 200px;
}
.cube {
position : relative;
width : 200px;
height : 200px;
transform-style: preserve-3d;
}
.panel {
position : absolute;
border : 1px solid #f00;
width : 200px;
height : 200px;
box-sizing : border-box;
}
.front {
background: rgba(255, 0, 0, 0.7);
}
.back {
background: rgba(0, 0, 255, 0.7);
}
.left {
background: rgba(255, 255, 0, 0.7);
}
.right {
background: rgba(0, 255, 255, 0.7);
}
.top {
background: rgba(0, 255, 0, 0.7);
}
.bottom {
background: rgba(255, 0, 255, 0.7);
}div.panelの6つなので、div.cubeにtransform-style: preserve-3dを指定します。
この時点では次のようになります。
.frontは最初から外を向いているので変更なし.backはY軸を中心に180度.leftはY軸を中心に90度.rightはY軸を中心に-90度.topはX軸を中心に90度.bottomはX軸を中心に-90度.front {
background: rgba(255, 0, 0, 0.7);
}
.back {
background: rgba(0, 0, 255, 0.7);
transform : rotateY(180deg);
}
.left {
background: rgba(255, 255, 0, 0.7);
transform : rotateY(90deg);
}
.right {
background: rgba(0, 255, 255, 0.7);
transform : rotateY(-90deg);
}
.top {
background: rgba(0, 255, 0, 0.7);
transform : rotateX(90deg);
}
.bottom {
background: rgba(255, 0, 255, 0.7);
transform : rotateX(-90deg);
}

前に説明したように、回転済みのものを移動するときには要素と共に回転した軸を考慮する必要があります。ここで、各パネルの表が外側を向くように回転させていますので、どのパネルも移動する方向はZ軸の正の方向になります。.front {
background: rgba(255, 0, 0, 0.7);
transform : translateZ(100px);
}
.back {
background: rgba(0, 0, 255, 0.7);
transform : rotateY(180deg) translateZ(100px);
}
.left {
background: rgba(255, 255, 0, 0.7);
transform : rotateY(90deg) translateZ(100px);
}
.right {
background: rgba(0, 255, 255, 0.7);
transform : rotateY(-90deg) translateZ(100px);
}
.top {
background: rgba(0, 255, 0, 0.7);
transform : rotateX(90deg) translateZ(100px);
}
.bottom {
background: rgba(255, 0, 255, 0.7);
transform : rotateX(-90deg) translateZ(100px);
}
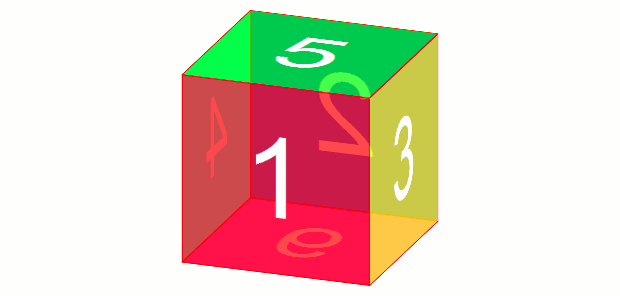
それでは、これをアニメーションで回転させます。アニメーションの指定については、以前書いた「CSSアニメーションの基礎」を参考にしてもらえればと思います。.cube {
position : relative;
width : 200px;
height : 200px;
transform-style: preserve-3d;
animation : rotation 4s linear infinite;
}
...
@keyframes rotation {
from {
transform: rotateY(0);
}
to {
transform: rotateY(360deg);
}
}
次は遠近感を出すためにPerspectiveを指定します。.cube {
position : relative;
width : 200px;
height : 200px;
transform-style: preserve-3d;
perspective : 500px;
animation : rotation 4s linear infinite;
}
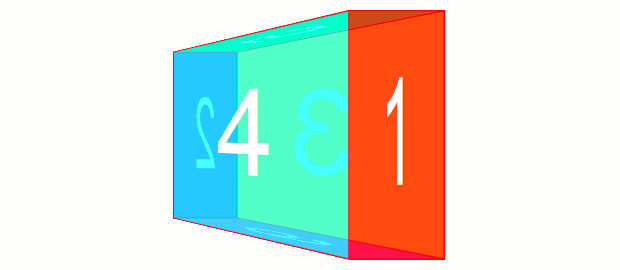
z=0から視点までの距離です。
この親要素を回転させると、Z軸も一緒に回転するわけで、それ伴ってPerspectiveでの視点も移動します。子要素はその回転する視点に合わせてを変形するので、このようなことになってしまったと考えられます。.cubeが回転する際にPerspectiveの視点が一緒に動いてしまわないようにすればいいのです。
つまり、.cubeの親、.drawingでperspectiveプロパティによる指定をしてしまえば、その視点は動かないわけですから、遠近感のある立方体ができあがるはずです。.drawing {
width : 200px;
perspective: 500px;
}
.cube {
position : relative;
width : 200px;
height : 200px;
transform-style: preserve-3d;
animation : rotation 4s linear infinite;
}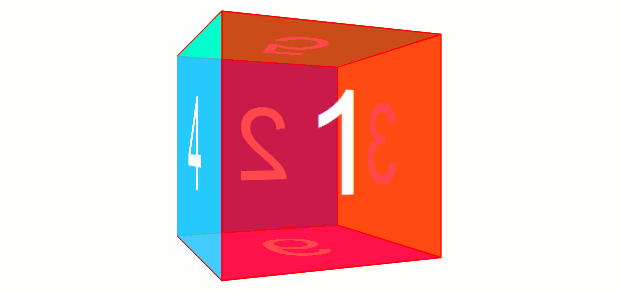

また、transformにperspective()関数で指定する場合には、回転の前に書かなければなりません。
ここではキーフレームの指定の中にあります。/* CSS Cube 7(これは上手くいかない) */
@keyframes rotation {
from {
transform: rotateY(0) perspective(500px);
}
to {
transform: rotateY(360deg) perspective(500px);
}
}
/* CSS Cube 8(期待通り) */
@keyframes rotation {
from {
transform: perspective(500px) rotateY(0);
}
to {
transform: perspective(500px) rotateY(360deg);
}
}
もしパネルの裏面を表示したくなければ、.panelにbackface-visibility: hiddenを指定してください。最後に
仕様が変更されるかもしれませんし、そもそも記事に誤りがある可能性もあります。